GEO Type Documentation

Geospatial types are special data types in databases used to store and manipulate geospatial data, which can represent geometric objects such as points, lines, and polygons.

Core purposes:
- Store geographic location information (e.g., longitude and latitude).
- Support spatial queries (e.g., distance calculation, area inclusion, intersection judgment).
- Process geospatial analysis (e.g., buffer analysis, path planning). Geographic Information Systems are widely used in map services, logistics scheduling, location-based social networking, meteorological monitoring, etc. The core requirement is to efficiently store massive spatial data and support low-latency spatial computing.

Core Encoding Technologies

S2 Geometry Library

S2 Geometry is a spherical geometry encoding system developed by Google. Its core idea is to achieve efficient indexing of global geospatial data through projection from a sphere to a plane.

Core Principles

Spherical projection: Project the Earth's sphere onto the 6 faces of a regular hexahedron, converting 3D spherical data into 2D planar data.
Hierarchical grid division: Each face is recursively divided into quadrilateral grids (cells), and each cell can be further subdivided into 4 smaller sub-cells, forming a hierarchical structure with 30 levels of precision (the higher the level, the smaller the cell area and the higher the precision).
64-bit encoding: Each cell is assigned a unique 64-bit ID, through which spatial positions can be quickly located and spatial relationships can be judged.
Hilbert curve ordering: Hilbert space-filling curves are used to encode cells, making spatially adjacent cells have continuous IDs and optimizing range query performance.

Advantages

High precision and smooth transition: 30 levels of hierarchy, with precision ranging from global (level 0) to centimeter-level (level 30), ensuring smooth transition to meet the needs of different scenarios.
Efficiency in global range queries: Suitable for large-scale spatial queries (e.g., cross-continental, cross-country regional analysis) with no significant performance degradation.
Efficient spatial relationship calculation: Inclusion, intersection, and other relationships can be quickly judged through cell IDs, avoiding complex geometric operations.

GeoHash Encoding

GeoHash is a geocoding method based on equirectangular projection, which realizes spatial indexing by converting longitude and latitude into strings.

Core Principles

Planar projection: Approximate the Earth's sphere as a plane, and recursively divide the area through binary division of longitude and latitude.
Rectangular grid division: Divide the Earth's surface into rectangular cells with different precisions. The length of the string determines the precision (up to 12 characters), and each additional character increases the precision by approximately 10 times.
Z-order curve encoding: Form a Z-order curve by alternately truncating the binary bits of longitude and latitude, converting 2D coordinates into 1D strings.

Features

Indexing convenience: Adjacent areas can be quickly queried through string prefix matching (e.g., GeoHash codes with the same prefix correspond to spatially adjacent areas).
Limitations:
- Limited precision levels: Up to 12 levels, with steep transitions between levels, making it difficult to meet the needs of high-precision smooth division.
- Mutability of Z-order curves: Spatially adjacent areas may have discontinuous codes due to curve jumps, affecting the accuracy of range queries.
- Low efficiency in large-scale queries: When querying global ranges, a large number of discrete cells need to be scanned, resulting in poor performance.

Comprehensive Comparison and Selection

Comprehensively comparing the characteristics of S2 Geometry Library and GeoHash, we choose S2 Geometry Library as the third-party dependency for geospatial processing, mainly for the following reasons:

Adaptability to global range queries: S2's hierarchical grid design is more suitable for large-scale spatial analysis, while GeoHash has performance bottlenecks in cross-region queries.
Precision and smoothness: S2's 30-level hierarchy can achieve smooth transition from global to centimeter-level, meeting multi-scenario precision requirements, which is better than GeoHash's 12-level division.
Spatial continuity: Hilbert curves have better spatial continuity than Z-order curves, which can reduce redundant calculations in range queries.

Introduction to WKT

WKT (Well-Known Text) is a standard text format for representing geospatial data.

Definition

Text format: Describe the structure and coordinates of geometric objects with text strings.
Features: Human-readable, easy to edit, suitable for manual input or simple data exchange.

Syntax Structure

Basic format: GeometryType(CoordinateValues)
Common geometric types:
- Point: POINT(longitude, latitude)
  Example: POINT(112.46, 45.23) represents the longitude and latitude of a point.
- LineString: LINESTRING(point1, point2)
  Example: LINESTRING(0 0, 1 1) represents a line segment connecting two points.
- Polygon: POLYGON ((0 0, 10 0, 10 10, 0 10, 0 0))

Introduction to WKB

WKB (Well-Known Binary) is a standard binary data format for representing geospatial data.

Definition

Binary format: Represent geometric objects with binary encoding, which is more compact and efficient than WKT.
Features: Optimized for internal storage and transmission by computers, saving space and enabling fast parsing.

Encoding Structure

WKB consists of the following parts:

Byte order (1 byte):
- 0x00: Big Endian (network byte order)
- 0x01: Little Endian (common in Intel/AMD architectures)
Geometry type (4-byte integer):
- 1: Point
- 2: LineString
- 3: Polygon
- ... (other types)
Coordinate values:
- Point: x, y (or x, y, z)
- LineString: coordinates of point1, coordinates of point2
- Polygon: coordinates of point1, coordinates of point2...

Example

    01 01 00 00 00 00 00 00 00 00 F0 3F 00 00 00 00 00 00 00 40
    └─┘ └─┘ └───────────────┘ └───────────────┘
    │   │         │               │
    Little Endian Point type     x=1.0           y=2.0

GeoPoint Type

Storing WKT Format Using String or Varchar

CREATE TABLE simple_point (  id INT,  wkt STRING) ;
INSERT INTO simple_point VALUES(1,'POINT(121.4737 31.2304)');

create table simple_point(id int, wkt VARCHAR(255);
INSERT INTO simple_point VALUES(1,'POINT(121.4737 31.2304)');

Querying WKT Format

select st_astext(st_geometryfromtext(wkt)) from simple_point;
+-------------------------------------+
| st_astext(st_geometryfromtext(wkt)) |
+-------------------------------------+
| POINT (121.4737 31.2304)            |
+-------------------------------------+

Storing Using WKB Format

CREATE TABLE simple_point (  id INT,  wkb STRING) ;
INSERT INTO simple_point VALUES(1,'\x01010000005f07ce19515e5e4097ff907efb3a3f40');

create table simple_point(id int, wkb VARCHAR(255);
INSERT INTO simple_point VALUES(1,'\x01010000005f07ce19515e5e4097ff907efb3a3f40');

Querying WKB Format

select st_astext(st_geometryfromwkb(wkb)) from simple_point;
+------------------------------------+
| st_astext(st_geometryfromwkb(wkb)) |
+------------------------------------+
| POINT (121.4737 31.2304)           |
+------------------------------------+

Storing Coordinates Using Floating-Point Numbers (x for latitude, y for longitude)

CREATE TABLE simple_point_double (id INT,x DOUBLE,y DOUBLE) 
INSERT INTO simple_point_double VALUES(0,1,2);

Querying Floating-Point Format

select st_astext(st_point(x,y)) from simple_point_double;
+--------------------------+
| st_astext(st_point(x,y)) |
+--------------------------+
| POINT (1 2)              |
+--------------------------+

GeoLine type

Storing WKT Format Using String or Varchar

CREATE TABLE simple_line (  id INT,  wkt STRING）
INSERT INTO simple_line VALUES(1,'LINESTRING(116.4074 39.9042, 121.4737 31.2304)');

CREATE TABLE simple_line (  id INT,  wkt VARCHAR(255)）
INSERT INTO simple_line VALUES(1,'LINESTRING(116.4074 39.9042, 121.4737 31.2304)');

Querying WKT Format

select st_astext(st_linefromtext(wkt)) from simple_line;
+-------------------------------------------------+
| st_astext(st_linefromtext(wkt))                 |
+-------------------------------------------------+
| LINESTRING (116.4074 39.9042, 121.4737 31.2304) |
+-------------------------------------------------+

Storing Using WKB Format

CREATE TABLE simple_line (  id INT,  wkb STRING）
INSERT INTO simple_line VALUES(1,'\x010200000002000000fc1873d7121a5d4088855ad3bcf343405f07ce19515e5e4097ff907efb3a3f40');

CREATE TABLE simple_line (  id INT,  wkb VARCHAR(255)）
INSERT INTO simple_line VALUES(1,'\x010200000002000000fc1873d7121a5d4088855ad3bcf343405f07ce19515e5e4097ff907efb3a3f40');

Querying WKB Format

select st_astext(st_geometryfromwkb(wkb)) from simple_line;
+-------------------------------------------------+
| st_astext(st_geometryfromwkb(wkb))              |
+-------------------------------------------------+
| LINESTRING (116.4074 39.9042, 121.4737 31.2304) |
+-------------------------------------------------+

GeoPolygon type

Storing WKT Format Using String or Varchar

CREATE TABLE simple_polygon (  id INT,  wkt STRING）
INSERT INTO simple_polygon VALUES(1,'POLYGON((0 0, 0 10, 10 10, 10 0, 0 0))');

CREATE TABLE simple_polygon (  id INT,  wkt VARCHAR(255)）
INSERT INTO simple_polygon VALUES(1,'POLYGON((0 0, 0 10, 10 10, 10 0, 0 0))');

Querying WKT Format

select st_astext(st_polygon(wkt)) from simple_polygon;
+------------------------------------------+
| st_astext(st_polygon(wkt))               |
+------------------------------------------+
| POLYGON ((10 0, 10 10, 0 10, 0 0, 10 0)) |
+------------------------------------------+

Storing Using WKB Format

CREATE TABLE simple_polygon_wkb (  id INT,  wkb STRING）
INSERT INTO simple_polygon_wkb VALUES(1,'\x010300000001000000050000000000000000002440000000000000000000000000000024400000000000002440000000000000000000000000000024400000000000000000000000000000000000000000000024400000000000000000');

CREATE TABLE simple_polygon_wkb (  id INT,  wkb VARCHAR(255)）
INSERT INTO simple_polygon_wkb VALUES(1,'\x010300000001000000050000000000000000002440000000000000000000000000000024400000000000002440000000000000000000000000000024400000000000000000000000000000000000000000000024400000000000000000');

Querying WKB Format

select st_astext(st_geometryfromwkb(wkb)) from simple_polygon_wkb;
+------------------------------------------+
| st_astext(st_geometryfromwkb(wkb))       |
+------------------------------------------+
| POLYGON ((10 0, 10 10, 0 10, 0 0, 10 0)) |
+------------------------------------------+

GeoMultiPolygon type

Storing WKT Format Using String or Varchar

CREATE TABLE simple_multipolygon (  id INT,  wkt STRING）
INSERT INTO simple_multipolygon VALUES(1,'MULTIPOLYGON(((0 0, 0 10, 10 10, 10 0, 0 0)),((20 20, 20 30, 30 30, 30 20, 20 20)))');

CREATE TABLE simple_multipolygon (  id INT,  wkt VARCHAR(255)）
INSERT INTO simple_multipolygon VALUES(1,'MULTIPOLYGON(((0 0, 0 10, 10 10, 10 0, 0 0)),  -- 第一个多边形((20 20, 20 30, 30 30, 30 20, 20 20))  -- 第二个多边形)');

Querying WKT Format

select st_astext(st_geometryfromtext(wkt)) from simple_multipolygon;
+----------------------------------------------------------------------------------------+
| st_astext(st_geometryfromtext(wkt))                                                    |
+----------------------------------------------------------------------------------------+
| MULTIPOLYGON (((10 0, 10 10, 0 10, 0 0, 10 0)), ((30 20, 30 30, 20 30, 20 20, 30 20))) |
+----------------------------------------------------------------------------------------+

Note: WKB format conversion for GeoMultiPolygon is not yet supported

GeoCircle type

Storage Method (Storing Center Coordinates and Radius Using Floating-Point Numbers) Since circles do not conform to WKB and WKT formats, three floating-point numbers are needed to store the center coordinates (x, y) and radius (R) respectively:

create table simple_circle(id int, X double,Y double, R double)
INSERT INTO simple_circle VALUES(1,1.0,1.0,2);

Query circle

select st_astext(st_circle(X,Y,R)) from simple_circle;
+-----------------------------+
| st_astext(st_circle(X,Y,R)) |
+-----------------------------+
| CIRCLE ((1 1), 2)           |
+-----------------------------+

Constraints

Index

Since Doris does not directly implement the Geo type but stores and converts it using WKT and WKB, query acceleration for GEO type queries through indexing technology is not possible.

Only 13-digit precision can be guaranteed when converting WKT to GEO output:

mysql> SELECT ST_AsText(ST_GeometryFromText("POINT (1 3.1415926535897223)"));
+----------------------------------------------------------------+
| ST_AsText(ST_GeometryFromText("POINT (1 3.1415926535897223)")) |
+----------------------------------------------------------------+
| POINT (1 3.14159265358972)                                     |
+----------------------------------------------------------------+

Only 13-digit precision can be guaranteed when converting binary to GEO output:

mysql> select ST_AsText(ST_GeomFromWKB(ST_AsBinary(ST_Point(24.7,3.141592653589793))));
+--------------------------------------------------------------------------+
| ST_AsText(ST_GeomFromWKB(ST_AsBinary(ST_Point(24.7,3.141592653589793)))) |
+--------------------------------------------------------------------------+
| POINT (24.7 3.1415926535898)                                             |
+--------------------------------------------------------------------------+

Common Uses and Methods of Geo Types in Doris

Calculating Distance Between Two Points on Earth

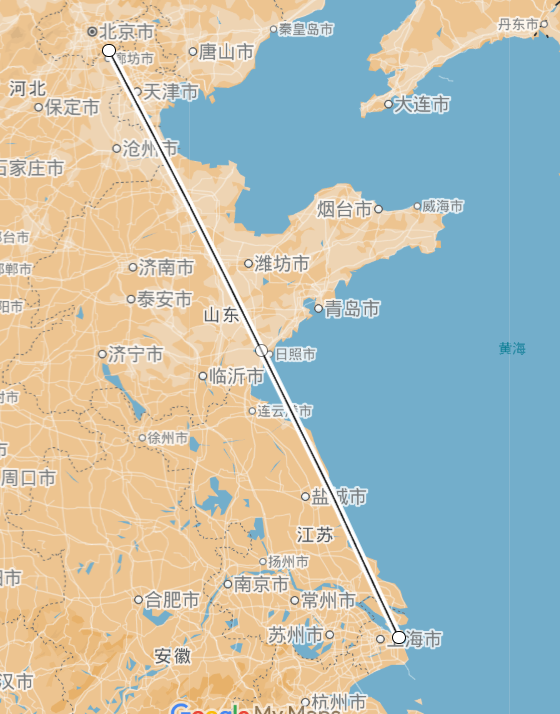
The distance of Beijing to Shanghai Coordinates of Beijing (116.4074, 39.9042) and Shanghai (121.4737, 31.2304):

select ST_DISTANCE_SPHERE(116.4074, 39.9042, 121.4737, 31.2304);
+----------------------------------------------------------+
| ST_DISTANCE_SPHERE(116.4074, 39.9042, 121.4737, 31.2304) |
+----------------------------------------------------------+
|                                       1067311.8461903075 |
+----------------------------------------------------------+

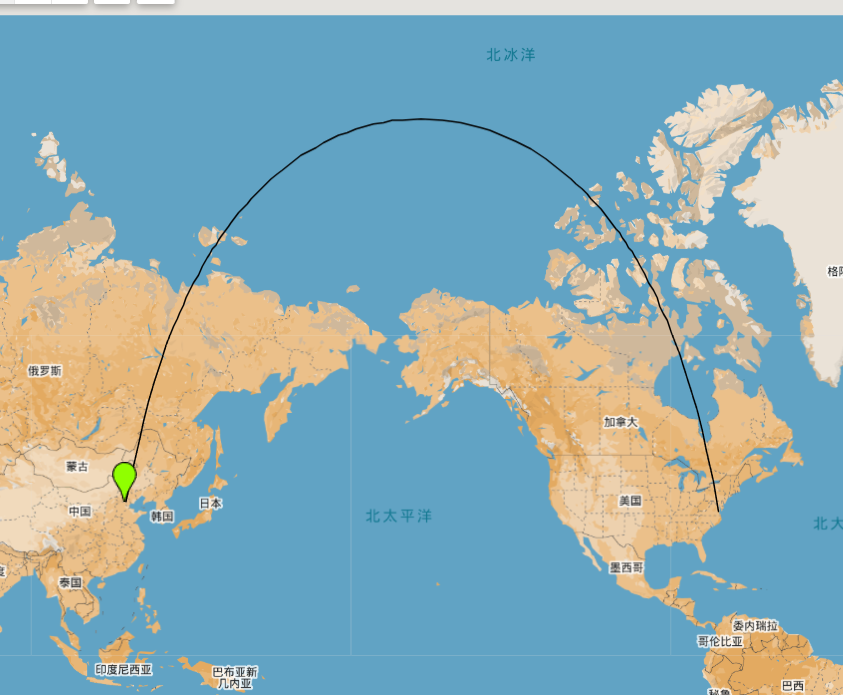
alt text

Distance of Beijing to New York Coordinates of Beijing (116.4074, 39.9042) and New York (-74.0060, 40.7128):

select ST_DISTANCE_SPHERE(116.4074, 39.9042, -74.0060, 40.7128);
+----------------------------------------------------------+
| ST_DISTANCE_SPHERE(116.4074, 39.9042, -74.0060, 40.7128) |
+----------------------------------------------------------+
|                                       10989107.361809434 |
+----------------------------------------------------------+

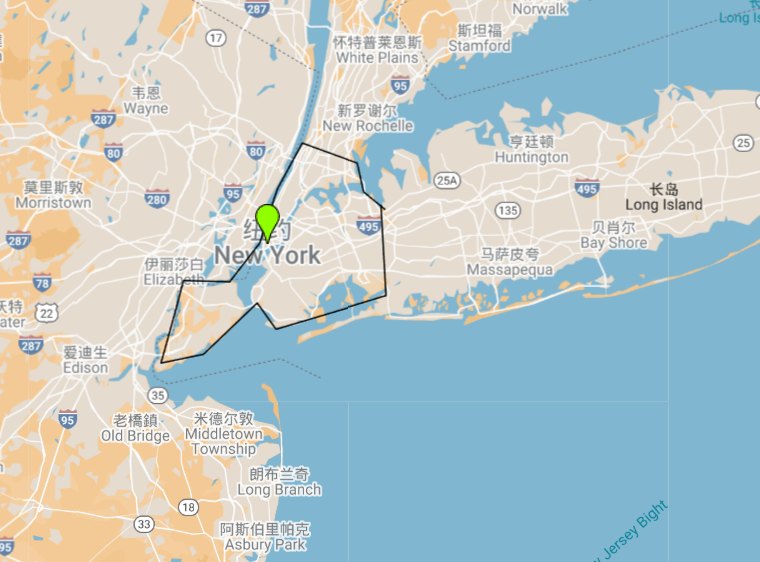
alt text

Calculating Area of a Region on the Earth's Sphere

Estimating New York's Area Outline the New York area roughly with a polygon and calculate the area:

SELECT ST_AREA_SQUARE_KM(
  ST_GeomFromText('POLYGON((
      -74.2591 40.9155, 
      -73.8726 40.9147, 
      -73.7004 40.7506, 
      -73.9442 40.5840, 
      -74.0817 40.6437, 
      -74.1502 40.6110, 
      -74.0984 40.6550, 
      -74.0431 40.7290, 
      -74.0136 40.7903, 
      -73.9352 40.8448, 
      -74.2591 40.9155
    ))'));
    
+-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+
| ST_AREA_SQUARE_KM(  ST_GeomFromText('POLYGON((-74.2591 40.9155, -73.8726 40.9147, -73.7004 40.7506, -73.9442 40.5840, -74.0817 40.6437,-74.1502 40.6110,-74.0984 40.6550,-74.0431 40.7290,-74.0136 40.7903,  -73.9352 40.8448, -74.2591 40.9155))'  )) |
+--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+
|                                                                                                                                                                                                                                      744.3806189617659 |
+-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+

alt text

Core Encoding Technologies

S2 Geometry Library​

Core Principles​

Advantages​

GeoHash Encoding​

Core Principles​

Features​

Comprehensive Comparison and Selection​

Introduction to WKT

Definition​

Syntax Structure​

Introduction to WKB

Definition​

Encoding Structure​

Example​

GeoPoint Type

GeoLine type

GeoPolygon type

GeoMultiPolygon type

GeoCircle type

Constraints

Index​

Common Uses and Methods of Geo Types in Doris

Calculating Distance Between Two Points on Earth​

Calculating Area of a Region on the Earth's Sphere​

S2 Geometry Library

Core Principles

Advantages

GeoHash Encoding

Core Principles

Features

Comprehensive Comparison and Selection

Definition

Syntax Structure

Definition

Encoding Structure

Example

Index

Calculating Distance Between Two Points on Earth

Calculating Area of a Region on the Earth's Sphere